¿QUE ES UN VECTOR?
Un vector puede utilizarse para representar una magnitud física, quedando definido por un modulo y una dirección u orientación. su expresión geométrica consiste en segmentos de recta dirigidos hacia un cierto lado, asemejándose a una flecha.
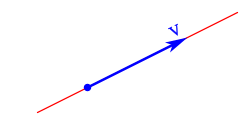
Características de un vector
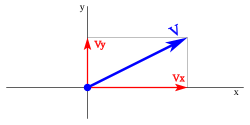
Un vector se puede definir por sus coordenadas, si el vector está en el plano xy, se representa
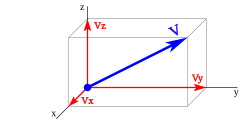
Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:
Si representamos el vector gráficamente podemos diferenciar los siguientes elementos:
El nombre o denominación es la letra, signo o secuencia de signos que define al vector.
El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.
El modulo o amplitud con una longitud proporcional al valor del vector.
La recta soporte o dirección, sobre la que se traza el vector.
Magnitudes vectoriales
Una magnitud escalar es aquella que queda completamente determinada con un número y sus correspondientes unidades, y una magnitud vectorial es aquella que, además de un valor numérico y sus unidades (módulo) debemos especificar su dirección y sentido.
Una magnitud escalar es aquella que queda completamente determinada con un número y sus correspondientes unidades, y una magnitud vectorial es aquella que, además de un valor numérico y sus unidades (módulo) debemos especificar su dirección y sentido.
Clasificación de vectores
Los vectores se clasifican en colineales, paralelos, perpendiculares, concurrentes, coplanarios, libres, deslizantes, opuestos, equipolentes, fijos y unitarios.
Colineales: Pertenecen o actúan sobre una misma línea recta, también se les llama linealmente dependientes y pueden ser verticales, horizontales e inclinados.
Paralelos: Tienen la misma dirección o inclinación.
Perpendiculares: dos vectores son perpendiculares entre sí cuando el ángulo entre ellos es 90°.
Concurrentes: Son vectores que al deslizarse sobre su línea de acción coinciden en un mismo punto del espacio.
Coplanarios: Actúan en un plano, por ejemplo el plano xy.
Libres: Se trasladan en cualquier punto del espacio manteniendo su módulo, dirección y sentido.
Deslizantes: Se trasladan a lo largo de la línea de acción determinada por su dirección.
Opuestos: Tienen el mismo módulo y dirección, y el sentido contrario.
Equipolentes: Tienen el mismo módulo, dirección y sentido.
Fijos: Tienen invariable el punto de aplicación.
Unitarios: Vectores cuyo módulo es la unidad.
Ejemplos de magnitudes vectoriales
Posición
La posición de un objeto o partícula con respecto a un sistema de referencia es un vector que viene dado por sus coordenadas rectangulares x, y, z, y se representa mediante sus componentes vectoriales xî, yĵ, zk. Los vectores î, ĵ, k son vectores unitarios.
Una partícula en un punto (x,y,z) tiene un vector de posición r = xî + yĵ + zk. El valor numérico del vector posición es r= √(x2 + y2 + z2). El cambio de posición de la partícula desde una posición a otra con respecto a un sistema de referencia es el vector Desplazamiento Δr y se calcula con la siguiente expresión vectorial:
Δr = r2 – r1
Aceleración
La aceleración media (am) se define como la variación de la velocidad v en un intervalo de tiempo Δt y la expresión para calcularla es am=Δv/Δt, siendo Δv el vector cambio de velocidad.
La aceleración instantánea (a) es el límite de la aceleración media am cuando Δt se hace tan pequeño que tiende a cero. La aceleración instantánea se expresa en función de sus componentes vectoriales
a =ax î +ay ĵ+ az k
Campo gravitacional
La fuerza de atracción gravitacional que ejerce una masa M, situada en el origen, sobre otra masa m en un punto del espacio x, y, z es un campo vectorial llamado campo de fuerza gravitacional. Esta fuerza viene dada por la expresión:
F=(-mMG/r)ȓ
r = xî + yĵ + zk
F = es la magnitud física fuerza gravitacional
G = es la constante de gravitación Universal
ȓ = es el vector de posición de la masa m
¿QUE SON LAS
COMPONENTES DE UN VECTOR?
Las componentes de un vector son las proyecciones de dicho vector sobre el eje coordenado; en la Figura vemos que vx y vy son las proyecciones del vector V sobre los ejes, por lo tanto, éstos son las componentes de V.
¿QUE
OPERACIONES SE PUEDEN REALIZAR CON UN VECTORES?
5 EJERCICIOS DE VECTORES
Ejercicio 1
Un vector 
tiene componentes 
. Hallar las coordenadas de 
si se conoce el extremo 
tiene componentes . Hallar las coordenadas de si se conoce el extremo Ejercicio 2
Dado el vector
y dos vectores equipolentes a 
y 
, determinar 
y 
sabiendo que 
y 
.
y dos vectores equipolentes a y , determinar y sabiendo que y .Ejercicio 3
Calcular la distancia entre los puntos 
y 
.
y .Ejercicio 4
Si 
es un vector de componentes 
, hallar un vector unitario de su misma dirección y sentido.
es un vector de componentes , hallar un vector unitario de su misma dirección y sentido.Ejercicio 5
Hallar un vector unitario de la misma dirección que el vector 
.
.
No hay comentarios:
Publicar un comentario